قاعدة ڤانت هوفت
معادلة ڤانت هوفت Van 't Hoff equation (تعرف أيضا باسم معادلة ڤوكانتشيتش ڤوكوڤيتش Vukancic-Vukovic equation) في الديناميكا الحرارية الكيميائية تربط التغير في درجة الحرارة (T) بالتغيير في ثابت الاتزان (k) معطية التغير في المحتوى الحراري القياسي (ΔH) للنظام. اشتق المعادلة للمرة الأولى العالم ياكوبوس ڤانت هوف وأثبتها لاحقاً گوران ڤوكانسيك وبورو ڤوكوفيتش.
يمكن كتابتة بالصيغة التالية أيضاً:
إذا افترضنا أن التغير في المحتوى الحراري للتفاعل يعتبر كثابت مع درجة الحرارة فإن التكامل المحدود للمعادلة التفاضلية في المعادلة ا1 وT2 يعطى بالمعادلة التالية
في هذه المعادلة (K(1 هو ثابت الاتزان في درجة الحرارة المطلقة T1 وK2 هو ثابت التوازن في درجة الحرارة المطلقة T2. و ΔH هو التغير في المحتوى الحراري القياسي و R هو ثابت الغاز.
وحيث
و
ويترتب على هذا
ولذلك، نضع اللوغاريتم الطبيعي لثابت توازن مقابل درجة الحرارة يعطي خط مستقيم. والميل للخط يساوي سالب التغير في المحتوى الحراري -ΔH القياسي مقسوماً على ثابت الغاز، -ΔH/R والتقاطع مساو للتغيير في الانتروبي القياسي مقسوماً على ثابت الغاز، ΔS/R. تفاضل هذه المعادلة الجبرية تعطي معادلة ڤانت هوفت.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
تطبيقات توقيع ڤانت هوفت
تحليل ڤانت هوفت
In biological research, the Van 't Hoff plot is also called Van 't Hoff analysis.[2] It is most effective in determining the favored product in a reaction. It may obtain results different from direct calorimetry such as differential scanning calorimetry or isothermal titration calorimetry due to various effects other than experimental error.[3]
Assume two products B and C form in a reaction:
- a A + d D → b B,
- a A + d D → c C.
In this case, Keq can be defined as ratio of B to C rather than the equilibrium constant.
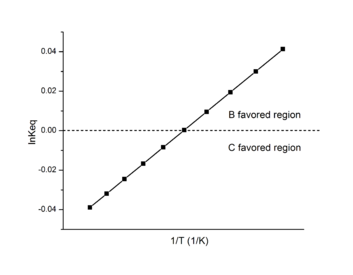
When B/C > 1, B is the favored product, and the data on the Van 't Hoff plot will be in the positive region.
When B/C < 1, C is the favored product, and the data on the Van 't Hoff plot will be in the negative region.
Using this information, a Van 't Hoff analysis can help determine the most suitable temperature for a favored product.
In 2010, a Van 't Hoff analysis was used to determine whether water preferentially forms a hydrogen bond with the C-terminus or the N-terminus of the amino acid proline.[4] The equilibrium constant for each reaction was found at a variety of temperatures, and a Van 't Hoff plot was created. This analysis showed that enthalpically, the water preferred to hydrogen bond to the C-terminus, but entropically it was more favorable to hydrogen bond with the N-terminus. Specifically, they found that C-terminus hydrogen bonding was favored by 4.2–6.4 kJ/mol. The N-terminus hydrogen bonding was favored by 31–43 J/(K mol).
This data alone could not conclude which site water will preferentially hydrogen-bond to, so additional experiments were used. It was determined that at lower temperatures, the enthalpically favored species, the water hydrogen-bonded to the C-terminus, was preferred. At higher temperatures, the entropically favored species, the water hydrogen-bonded to the N-terminus, was preferred.
دراسات ميكانيكية
A chemical reaction may undergo different reaction mechanisms at different temperatures.[5]
In this case, a Van 't Hoff plot with two or more linear fits may be exploited. Each linear fit has a different slope and intercept, which indicates different changes in enthalpy and entropy for each distinct mechanisms. The Van 't Hoff plot can be used to find the enthalpy and entropy change for each mechanism and the favored mechanism under different temperatures.
In the example figure, the reaction undergoes mechanism 1 at high temperature and mechanism 2 at low temperature.
الاعتماد على درجة الحرارة
If the enthalpy and entropy are roughly constant as temperature varies over a certain range, then the Van 't Hoff plot is approximately linear when plotted over that range. However, in some cases the enthalpy and entropy do change dramatically with temperature. A first-order approximation is to assume that the two different reaction products have different heat capacities. Incorporating this assumption yields an additional term c/T2 in the expression for the equilibrium constant as a function of temperature. A polynomial fit can then be used to analyze data that exhibits a non-constant standard enthalpy of reaction:[6]
where
Thus, the enthalpy and entropy of a reaction can still be determined at specific temperatures even when a temperature dependence exists.
Surfactant self-assembly
The Van 't Hoff relation is particularly useful for the determination of the micellization enthalpy ΔH⊖m of surfactants from the temperature dependence of the critical micelle concentration (CMC):
However, the relation loses its validity when the aggregation number is also temperature-dependent, and the following relation should be used instead:[7]
with GN + 1 and GN being the free energies of the surfactant in a micelle with aggregation number N + 1 and N respectively. This effect is particularly relevant for nonionic ethoxylated surfactants[8] or polyoxypropylene–polyoxyethylene block copolymers (Poloxamers, Pluronics, Synperonics).[9] The extended equation can be exploited for the extraction of aggregation numbers of self-assembled micelles from differential scanning calorimetric thermograms.[10]
انظر أيضاً
المصادر
- ^ Atkins, Peter; De Paula, Julio (2006-03-10). Physical Chemistry (8th ed.). W.H. Freeman and Company. p. 212. ISBN 0716787598.
- ^ "Van 't Hoff Analysis". Protein Analysis and Design Group.
- ^ Cooper, Alan (2018), Roberts, Gordon; Watts, Anthony, eds. (in en), Van’t Hoff Analysis and Hidden Thermodynamic Variables, Berlin, Heidelberg: Springer, pp. 1–4, doi:, ISBN 978-3-642-35943-9, https://doi.org/10.1007/978-3-642-35943-9_10066-1, retrieved on 2023-07-04
- ^ Prell, James; Williams E. (2010). "Entropy Drives an Attached Water Molecule from the C- to N-Terminus on Protonated Proline". J. Am. Chem. Soc. 132 (42): 14733–5. doi:10.1021/ja106167d. PMID 20886878.
- ^ Chatake, Toshiyuki (2010). "An Approach to DNA Crystallization Using the Thermal Reversible Process of DNA Duplexes". Cryst. Growth Des. 10 (3): 1090. doi:10.1021/cg9007075.
- ^ David, Victor (28 April 2011). "Deviation from van 't Hoff dependence in RP-LC induced by tautomeric interconversion observed for four compounds". Journal of Separation Science. 34 (12): 1423–8. doi:10.1002/jssc.201100029. PMID 21538875.
- ^ Holtzer, Alfred; Holtzer, Marilyn F. (2002-05-01). "Use of the van 't Hoff relation in determination of the enthalpy of micelle formation". The Journal of Physical Chemistry (in الإنجليزية). 78 (14): 1442–1443. doi:10.1021/j100607a026.
- ^ Heerklotz, Heiko; Tsamaloukas, Alekos; Kita-Tokarczyk, Katarzyna; Strunz, Pavel; Gutberlet, Thomas (2004-11-25). "Structural, Volumetric, and Thermodynamic Characterization of a Micellar Sphere-to-Rod Transition". Journal of the American Chemical Society (in الإنجليزية). 126 (50): 16544–16552. doi:10.1021/ja045525w. PMID 15600359.
- ^ Taboada, Pablo; Mosquera, Victor; Attwood, David; Yang, Zhuo; Booth, Colin (2003-06-05). "Enthalpy of micellisation of a diblock copoly(oxyethylene/oxypropylene) by isothermal titration calorimetry. Comparison with the Van 't Hoff value". Physical Chemistry Chemical Physics (in الإنجليزية). 5 (12): 2625–2627. Bibcode:2003PCCP....5.2625T. doi:10.1039/b303108j.
- ^ Chiappisi, Leonardo; Lazzara, Giuseppe; Gradzielski, Michael; Milioto, Stefana (2012-12-06). "Quantitative Description of Temperature Induced Self-Aggregation Thermograms Determined by Differential Scanning Calorimetry" (PDF). Langmuir (in الإنجليزية). 28 (51): 17609–17616. doi:10.1021/la303599d. hdl:10447/96872. PMID 23171124.







![{\displaystyle {\begin{aligned}\Delta _{r}H_{1}&=-R\times {\text{slope}}_{1},&\Delta _{r}S_{1}&=R\times {\text{intercept}}_{1};\\[5pt]\Delta _{r}H_{2}&=-R\times {\text{slope}}_{2},&\Delta _{r}S_{2}&=R\times {\text{intercept}}_{2}.\end{aligned}}}](https://www.marefa.org/api/rest_v1/media/math/render/svg/2b7e4e668b82b9ee277ed6bf1aaae55cb12f15a8)




