قانون سنيل

إنكسار الضوء بين وسطين مختلفي معامل الإنكسار.

في البصريات، قانون سنيل إنگليزية: Snell's law، (ويعرف أيضا بقانون سنيل - ديكارت)، هو صيغة رياضية تصف العلاقة ما بين زوايا الإنعكاس والإنكسار، عندما ينتقل الضوء أو غيره من الأمواج ما بين وسطين مختلفين، مثل الهواء والماء. وبموجب هذا القانون، تكون نسبة جيوب زوايا الإنعكاس أو الإنكسار قيمة ثابتة مرتبطة بطبيعة الوسط الذي تعبره الأمواج. ينطبق هذا القانون على تنقل الأمواج في أوساط متجانسة ومتماثلة الخصائص في كل الإتجاهات.

يقوم قانون سنيل على مبدئين هما:

• توجد جميع الأمواج الساقطة والمنعكسة والمنكسرة على نفس السطح.
• إذا كانت $\theta _{1}$ هي زاوية سقوط الموجة على السطح الواصل بين الوسطين $(1)$ و$(2)$، و $\theta _{2}$ هي زاوية إنكسار، و$v_{2}$ و$v_{1}$، هما سرعتا الموجة تباعا في الوسطين $(1)$ و$(2)$، يكتب قانون سنيل كالآتي :

${\frac {\sin \theta _{1}}{\sin \theta _{2}}}={\frac {v_{1}}{v_{2}}}={\frac {n_{2}}{n_{1}}}$

أو

$n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}\$ حيث $n_{1}$ و$n_{2}$ معاملا الإنكسار تباعا في الوسطين $(1)$ و$(2)$.

إذا كان معامل إنكسار الوسط الأول أصغر من معامل إنكسار الوسط الثاني، أي أن سرعة الموجة في هذا الأخير تقل، مثل المرور من الهواء إلى الماء أو الزجاج، فإن زاوية الإنكسار تكون أقل من زاوية السقوط، والعكس بالعكس.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 التاريخ

نسخة من صفحة من مخطوط ابن سهل توضح اكتشافه لقانون الانكسار.

بطليموس، اليوناني المقيم في الإسكندرية، اكتشف علاقة عن زوايا الانكسار، إلا أنها لم تكن دقيقة للزوايا غير الصغيرة. كان بطليموس واثقاً أنه قد توصل لقانون وضعي دقيق، جزئياً بسبب تحويره للبيانات لتتفق مع نظريته (انظر: confirmation bias). أما ابن الهيثم، في كتابه كتاب المناظر (1021)، فقد كان أكثر قرباً لاكتشاف قانون الانكسار، بالرغم من أنه لم يأخذ خطوة وضع القانون.

وجهة نظر من عام 1837 عن تاريخ "قانون الجيوب"

The law of refraction was first accurately described by ابن سهل, of بغداد, in the manuscript On Burning Mirrors and Lenses (984). He made use of it to work out the shapes of lenses that focus light with no geometric aberrations, known as anaclastic lenses.

أعيد اكتشاف القانون من قِبل توماس هاريوت في 1602، who however did not publish his results although he had corresponded with Kepler on this very subject. In 1621, Willebrord Snellius (Snel) derived a mathematically equivalent form, that remained unpublished during his lifetime. René Descartes independently derived the law using heuristic momentum conservation arguments in terms of sines in his 1637 treatise Discourse on Method, and used it to solve a range of optical problems. Rejecting Descartes' solution, Pierre de Fermat arrived at the same solution based solely on his principle of least time.

According to Dijksterhuis, "In De natura lucis et proprietate (1662) Isaac Vossius said that Descartes had seen Snell's paper and concocted his own proof. We now know this charge to be undeserved but it has been adopted many times since." Both Fermat and Huygens repeated this accusation that Descartes had copied Snell.

In French, Snell's Law is called "la loi de Descartes" or "loi de Snell-Descartes."

رسم كريستيان هويگنز

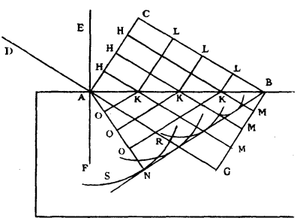
في كتابه لعام 1678 Traité de la Lumiere، بيـَّن كريستيان هويگنز كيف أن قانون سنـِل للجيوب يمكن شرحه بواسطة، أو اشتقاقه من، الطبيعة الموجية للضوء، باستخدام ما صرنا نسميه مبدأ هويگنز-فرنل.

 الاشتقاقات والصيغ

جبهات موجية من مصدر نقطي في سياق قانون سنـِل. المنطقة أسف الخط الرمادي لها مؤشر انكسار أكبر، ونسبياً سرعة ضوء أقل، عن المنطقة أعلى الخط.

$k_{x{\text{Region}}_{1}}=k_{x{\text{Region}}_{2}}\,$

$n_{1}k_{0}\sin \theta _{1}=n_{2}k_{0}\sin \theta _{2}\,$

$n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}\,$

where $k_{0}={\frac {2\pi }{\lambda _{0}}}={\frac {\omega }{c}}$ is the wavenumber in vacuum. Note that no surface is truly homogeneous, in the least at the atomic scale. Yet full translational symmetry is an excellent approximation whenever the region is homogeneous on the scale of the light wavelength.

 الصيغة المتجهية

Given a normalized light vector l (pointing from the light source toward the surface) and a normalized plane normal vector n, one can work out the normalized reflected and refracted rays:

$\cos \theta _{1}=\mathbf {n} \cdot (-\mathbf {l} )$

$\cos \theta _{2}={\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\right)^{2}\left(1-\left(\cos \theta _{1}\right)^{2}\right)}}$

$\mathbf {v} _{\mathrm {reflect} }=\mathbf {l} +\left(2\cos \theta _{1}\right)\mathbf {n}$

$\mathbf {v} _{\mathrm {refract} }=\left({\frac {n_{1}}{n_{2}}}\right)\mathbf {l} +\left({\frac {n_{1}}{n_{2}}}\cos \theta _{1}-\cos \theta _{2}\right)\mathbf {n}$

Note: $\mathbf {n} \cdot (-\mathbf {l} )$ must be positive. Otherwise, use

$\mathbf {v} _{\mathrm {refract} }=\left({\frac {n_{1}}{n_{2}}}\right)\mathbf {l} +\left(-{\frac {n_{1}}{n_{2}}}\cos \theta _{1}+\cos \theta _{2}\right)\mathbf {n} .$

مثال:

$\mathbf {l} =\{0.707107,-0.707107\},~\mathbf {n} =\{0,1\},~{\frac {n_{1}}{n_{2}}}=0.9$

$\mathbf {~} \cos \theta _{1}=0.707107,~\cos \theta _{2}=0.771362$

$\mathbf {v} _{\mathrm {reflect} }=\{0.707107,0.707107\},~\mathbf {v} _{\mathrm {refract} }=\{0.636396,-0.771362\}$

The cosines may be recycled and used in the Fresnel equations for working out the intensity of the resulting rays.

Total internal reflection is indicated by a negative radicand in the equation for $\cos \theta _{2}$. In this case, an evanescent wave is produced, which rapidly decays from the surface into the second medium. Conservation of energy is maintained by the circulation of energy across the boundary, averaging to zero net energy transmission.

 الانعكاس الداخلي الكلي والزاوية الحرجة

Demonstration of no refraction at angles greater than the critical angle.

المقالة الرئيسية: Total internal reflection

For example, consider a ray of light moving from water to air with an angle of incidence of 50°. The refractive indices of water and air are approximately 1.333 and 1, respectively, so Snell's law gives us the relation

$\sin \theta _{2}={\frac {n_{1}}{n_{2}}}\sin \theta _{1}=1.333\cdot 0.766=1.021,$

which is impossible to satisfy. The critical angle θ_crit is the value of θ₁ for which θ₂ equals 90°:

$\theta _{\text{crit}}=\arcsin \left({\frac {n_{2}}{n_{1}}}\sin \theta _{2}\right)=\arcsin {\frac {n_{2}}{n_{1}}}=48.6^{\circ }.$

 انظر أيضاً

• Evanescent wave
• Fresnel equations
• Reflection (physics)
• Refraction
• Snell's window
• Total internal reflection
• Calculus of variations
• Brachistochrone curve for a simple proof by Jacob Bernoulli
• Hamiltonian optics

 وصلات خارجية

• Discovery of the law of refraction
• Snell's Law of Refraction (Wave Fronts) by Todd Rowland, Wolfram Demonstrations Project.
• Computation of radiowave attenuation in the atmosphere