ارتفاع (مثلث)
الارتفاع في المثلث هو الخط العمودي النازل من إحدى زوايا المثلث إلى الضلع المقابل لهذه الزاوية أو امتداد هذه الضلع. نقطة التقاطع بين الارتفاع و الضلع المقابل له يسمى قدم الارتفاع. الضلع المقابل للارتفاع يسمى قاعدة الارتفاع. طول الارتفاع هو البعد بين الرأس الصادر منه الارتفاع و قدمه.
- في مثلث متساوي الساقين يكون الارتفاع الصادر من الرأس يقطع الضلع المقابل له في منتصفه.
يمكننا الارتفاع كذلك من حساب مساحة المثلث أي جداء القاعدة في الارتفاع مقسومين على 2.
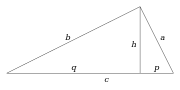
- في مثلث قائم الإرتفاع المقابل للوتر يقسمه إلى طولين p و q. لنرمز إلى طول الإرتفاع ب h فنستنتج العلاقة
- h2 = pq
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
حساب الارتفاع في مثلث قائم
لدينا ABC مثلث قائم في A و [AH] الارتفاع الصادر من A و الموافق ل[BC] إذاً نستنتج أنّ AH.BC=AB.AC التعليل: نستطيع حساب مساحة المثلث القائم بطريقتين: إمّا بحساب جداء الضلعين المتعامدين AB و AC (في المثلث السابق) ثم نقسم النتيجة على 2. أو نحسب جداء الإرتفاع الصادر من A أي [AH] في القاعدة [BC] ثمّ نقسم الحاصل على 2. فنستنتج أنّ AH.BC=AB.AC
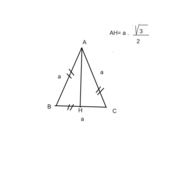
الارتفاع في مثلث متساوي الساقين
في مثلث متقايس الاضلاع أيّ إرتفاع قابل للقياس فقط بمعرفة طول ضلع المثلث حسب القاعدة المبينة في الرسم
 | هذه بذرة مقالة عن الهندسة الرياضية تحتاج للنمو والتحسين، ساهم في إثرائها بالمشاركة في تحريرها. |
