آلة تورنگ
| آلات | |
|---|---|
| علم | |
آلة تورنگ Turing machine هي عبارة جهاز يعامل مجموعة من الرموز المصفوفة على شريط وفق مجموعة من القواعد. سميت بهذا الإسم نسبة لعالم الرياضيات الإنكليزي آلان تورنگ الذي أوجد هذا النموذج سنة 1937م[1] الذي وصفها "بالآلة التلقائية" "a(utomatic)-machine". وعلى الرغم من بساطة هذا النموذج إلا أنه يمكن استخدامه لمحاكاة منطق أي خوارزمية حاسوبية. لا تعد آلة تورنگ تقنية حوسبة، ولكنها تجربة فكرية يستخدمها علماء الحاسوب لدراسة قدرات الحاسوب على حل مسائل التحسيب المختلفة ومحدوديات هذه القدرات، لذلك فهي من المفاهيم الأساسية في كل من نظرية الحسوبية ونظرية التعقيد التحسيبي.
ولقد قدم آلان تورنگ تعريفا موجزاً للتجربة في مقاله الذي نشره عام 1948 بعنوان "الآلات الذكية" "Intelligent Machinery"، حيث قال أن آلة تورنگ التي سماها آلة الحوسبة المنطقية، تتألف من:
... قدرة ذاكرة لانهائية يتم الحصول عليها في شكل شريط لانهائي مقسم إلى مربعات، حيث يمكن طباعة رمز ما عليه. في أي لحظة، يوجدرمز واحد فقط في الآلة، يسمى الرمز الممسوح. ويمكن للآلة تبديل ذلك الرمز الممسوح الذي يحدد، بشكل جزئي، سلوك الآلة، على العكس من رموز الشريط الموجودة في المربعات الأخرى التي لا تؤثر على سلوك الآلة. ومع ذلك ، يمكن نقل الشريط إلى الأمام وإلى الخلف من خلال الآلة نفسها، باعتبار هذه العملية من العمليات الابتدائية لها. Any symbol on the tape may therefore eventually have an innings. (تورينج 1948 ، ص 61)
إن آلة تورنگ القادرة على محاكاة أى من آلات تورنگ الأخرى تسمى آلة تورنگ العامة (UTM, أو ببساطة آلة عامة ). كما يوجد تعريف رياضي عام قدم بواسطة ألونزو تشيرش ، الذي أدى تداخل عمله في حساب لمبدا مع نظرية تورنگ الصورية للتحسيب إلى ظهور فرضية تشيرش-تورنگ.
وصف غير رسمي
- لتخيل آلات تورنج, أنظر معرض الصور لآلات تورنج.
إن آلة تورنگ تخلق نماذج رياضية , إنها آلة ميكانيكية تعمل على الشريط الذي تكون الرموز فيه قد كتبت حيث تستطيع القراءة والكتابة مرة واحدة في الوقت مستخدمة رأس للشريط. العملية كاملة تتحدد بواسطة مجموعة محدودة من الإرشادات أو التعليمات الإبتدائية مثل "فى الحالة 42, إذا كان الرمز المقروء هو الصفر, فأكتب "1"; إذا كان الرمز المقروء هو الواحد, فأنتقل إلى اليسار, و إنتقل إلى الحالة 17; في الحالة 17 , إذا كان الرمز المقروء هو الصفر, فأكتب "1"; و إنتقل إلى الحالة 6;" ..إلخ. في المقالة الأصلية ("فى الأرقام الخاضعة للحساب, و بتطبيق قرار المشكلة", أنظر أيضاالمراجع أنظر أسفل), تورينج لا يتصور آلة ميكانيكية ، ولكن بعتقد أنه شخصا الذي يدعوه "الكمبيوتر" ، الذي ينفذ هذه القواعد القطعية الميكانيكية صاغرا (أوكما وضعها تورنج, " على نحو منهجي").
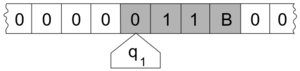
من خلال تصميم الآلة التي عرفت فيما بعد باسم (آلة تورنگ) Turing Machine، وهي نموذج مثالي لرياضي يعالج رموزاً رياضية، فيحول العبارات إلى عبارات بديلة، مقترباً من التوصل إلى حل لأي صيغة.
وصف الآلة
يمكن التعبير عنها من صيغ العمليات الحسابية. كان بالآلة شريط طويل لا نهائي يحتوي على خلايا متميزة كل منها يحتوي على رمز. وكان بالآلة أيضاً وحدة تستطيع قراءة أو كتابة تلك الرموز، مع تقرير موقع وقيمة الرمز المكتوب بواسطة مجموعة صغيرة من القواعد البسيطة بناء على القيم المقروءة. وتتحرك الوحدة بطول الشريط لقراءة الرموز وتغييرها من أجل تغيير محتويات الشريط من (المسألة) الأصلية إلى (الحل) النهائي. وعندما يتولد الحل النهائي، تتوقف آلة تورنگ. فأي مسألة تتوقف فيها الآلة تكون مسألة قابلة للحل أو (قابلة للحسم)، وأي مسألة لا تتوقف فيها الآلة تكون (غير قابلة للحسم).. لقد أثبت تورنج أن هناك عبارات رياضية جيدة الصياغة لن تصل الآلة في حلها إلى مرحلة التوقف أبداً، وبالتالي فإن هناك بالفعل عبارات غير قابلة للحسم. تعد آلة تورنگ فكرة في غاية الفعالية من حيث إنها تزود الرياضيين بطريقة آلية بسيطة لدراسة مهمتهم. ولكن آلة تورنگ التي يتم بناؤها فعلاً تعتبر أكثر فعالية إلى حد بعيد، فهي تتحول إلى رياضي آلي بالكلية أوحاسب آلي قابل للبرمجة وقادر على إنجاز أية عملية حسابية. ولعل أهم الخطوات التي اتخذت في هذا الاتجاه اتخذت على يد زميل تورنج السابق في برنستونPrinceton وهو جون فون نيومان John von Neumann. فقد أنتج نيومان التصميم اللازم لتنفيذ الآلة تصميماً ملموساً، ومن ثم أعطانا الحاسب الآلي الحديث. وبلغة الرياضيات، فإن أي برنامج حاسوبي ما هو إلا آلة تورنگ، و الحاسب الآلي أو الجهاز القادر على تشغيل آلة تورنگ من أي نوع يسمى آلة تورنگ عامة Universal Turing Machine، وهي عبارة عن نموذج رياضي قادر على تفسير أي نموذج رياضي. بيد أن احد ملامح العمل الذي قام به تورنج تمثل في بيان أن هناك برامج لا يمكن أن تصل إلى درجة التمام، وهي البرامج المناظرة لعبارة هذه العبارة خطأ، وبالتالي لا يمكن حسمها. فما الذي يعنيه هذا الأمر بالنسبة إلى أمن المعلومات؟ في الأساس نحن نريد أن نعرف مسبقاً ما إذا كان أي تسلسل بعينه من التغييرات الطارئة على البيانات وهي البرنامج سوف يكون ضارا أم غير ضار. لسوء الحظ أن فريد كوهين Fred Cohen تمكن في عام 1986 من إثبات أن مشكلة تقرير ما إذا كان أحد البرامج فيروساً أم لا هي مشكلة غير قابلة للحسم. فإذا قامت آلة تورنگ بإجراء تحليل لهذا البرنامج، فإنها لن تتوقف أبداً، والسبيل الوحيد إلى تقرير أثر البرنامج هو تشغيل هذا البرنامج فعلاً ورؤية ما يحدث. تعتبر هذه النتيجة ذات أهمية بالغة، فهي تعني أن مهمة البرنامج المضاد للفيروسات مهمة مستحيلة رياضياً. وبالقياس فإن مهمة التقرير المسبق لما إذا كان أي برنامج سيحدث أثراً ضاراً هي مهمة مستحيلة كذلك. والسبيل الوحيد للتوصل إلى طبيعة ما سيفعله البرنامج في الواقع يتمثل في السماح له بالعمل ثم فحص حالة ذاكرة الحاسب. فإذا كانت مهمة أمن المعلومات هي التنبؤ بما إذا كان برنامج بعينه سيكون له أثر ضار على حالة البيانات، إذن فهي مهمة مستحيلة. فحوى الكلام أن النموذج الرياضي للحوسبة يحتوي على مخاطر كامنة بداخله فنحن نعرف أننا لا نستطيع أن نعرف مسبقاً ما إذا كان شيء ما سيحدث ضرراً أم لا. وفي هذا الصدد أستعير عبارة الزميل ستيفن كاستيل Stephen Castell التي تقول إن الحواسب غير آمنة بطبيعتها، سواء أكانت مصممة وفق نموذج فون نيومان أو غيره من النماذج البنيوية.
انظر أيضاً
|
|
- المصدر [صحبفة العدالة العراقية
مراجع
- ^ The idea came to him in mid-1935 (perhaps, see more in the History section) after a question posed by M. H. A. Newman in his lectures -- "Was there a definite method, or as Newman put it, a mechanical process which could be applied to a mathematical statement, and which would come up with the answer as to whether it was provable" (Hodges 1983:93). Turing submitted his paper on 31 May 1936 to the London Mathematical Society for its Proceedings (cf Hodges 1983:112), but it was published in early 1937 -- offprints available February 1937 (cf Hodges 1983:129).
وصلات خارجية
| Turing machine
]].- Turing Machine on Stanford Encyclopedia of Philosophy
- Detailed info on the Church-Turing Hypothesis (Stanford Encyclopedia of Philosophy)
- Turing Machine-Like Models in Molecular Biology, to understand life mechanisms with a DNA-tape processor.
- The Turing machine—Summary about the Turing machine, its functionality and historical facts
- Can the cosmos be modeled by a Turing machine? Private web site concludes that the cosmos cannot be represented as a Turing computation.
- The Wolfram 2,3 Turing Machine Research Prize—Stephen Wolfram's $25,000 prize for the proof or disproof of the universality of the potentially smallest universal Turing Machine. The contest has ended, with the proof affirming the machine's universality.
- Turing Machine in Conway's Game of Life by Paul Rendell
- "Turing Machine Causal Networks" by Enrique Zeleny, Wolfram Demonstrations Project.
- Turing Machines at the Open Directory Project
- n bands Turing Machine Simulator

