نظرية الظلال

نظرية الظلال هي فرع من فروع الهندسة الوصفية، تستخدم في تمثيل ظلال الأجسام بالنسبة لمصدر ضوء. الظل هو منطقة محددة بمحيط مغلق ناتج عن وجود مصدر ضوء.
يمكن تعريف نظرية الظلال بالدراسة التي تسمح , عندما يثبت مصدر ضوء, بانشاء ، من خلال سلسلة من العمليات الرسومية الهندسية، الظل الذاتي والساقط لشكل ما [1]
تم التأكيد ان الهندسة الوصفية يجب ان تؤخذ في الاعتبار من وجهتين نظر. الأولى باعتبارها وسيلة للوصول الى تحديد بدقة النتائج المرجوة، وهذه هي الطريقة التي كانت تستخدم في قطع الحجارة والنجارة. من جهة ثانية ، فهي وسيلة إظهار للكيانات الهندسية. في هذه الحالة تحديد الظلال هي ميزة مساعدة.[2]
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
تاريخ
الدراسات الأولى عن الإنشاءات الهندسية للظلال في الاظهار المنظوري تعود إلى 1600 وبالخصوص الى كتب گويدوبالدو دل مونته عن الاظهار المنظوري (Perspectivae Libri VI)ء, 1600 بيزا.
على وجه الخصوص ، بالنسبة الى الإنشاءات الهندسية للظلال في الاسقاطات المتعامدة ، من المناسب الإشارة إلى دروس all'Ecoles Normales ل غاسبر مونج (القرنين الثامن عشر والتاسع عشر). تحديد الاشكال في الفراغ وطرق اظهارها هي مهمة الهندسة الوصفية التي هدفها حدد من قبل غاسبر مونج منذ البداية. من ضمن الرسومات التي نفذها مونج كان هناك أيضا جزء يتعلق بنظرية الظلال. على بينة ان الرسوم ليس لها معنى عندما تفتقر إلى تأثيرات الظلال. [3]. ومن الواضح ان الرسم مهما كان دقيق ولكنة يفتقر للظلال, يبدو غامض وغير محدد.
الاطروحات في مجال الهندسة الوصفية بعد مونج, تضمنت العديد من الدراسات التي كرست حيزا واسعا لموضوع الظلال، مثل، دراسات فاليه (1821- Vallee) [4] ، هاشيت (1828Hachette) [5]، بيليت (1885 Pillet) [6].
تم الانتهاء من عملية الترميز في اطروحة المنظور الخطي (Traite’ de la Perspective Lineaire) من عمل لا گورنير (La Gourneire -1862)
وقد نشرت في نظرية الظلال والكياروسكورو دراسات مثيرة للاهتمام في ايطاليا من قبل تساري (Tessari 1880) [7] , و بونتشي (Bonci 1937) [8].

الظل في الاظهار الهندسي
الظلال في التمثيل الهندسي يطبق لإعطاء ادراك بعمق الفراغ، اي لخلق وهمية البعد الثالث على سطح الرسم، وأيضاً لإعطاء صورة صحيحة عن موضع الجسم في الفراغ. ولهذا فعملية التظليل تتطلب معرفة دقيقة بقواعد الهندسة الوصفية, لتكوين الفراغ المعماري.
الظل الناتج من جسم K هو عملية إسقاط للجسم K من مركز إسقاط C متطابق مع مصدر الضوء. الذي يمكن أن يكون نقطة نهائية كمصباح كهربائي (أو شمعة), أو نقطة لانهائية كالشمس.
بما ان الظلال تنتج من عملية اسقاط, ففي الحالة التي يكون فيها مصدر الضوء C نقطة نهائية, تلك العملية تعتبر اسقاط مركزي, والا فهي اسقاط متوازي, اي عندما يكون C نقطة لانهائية.
الظلال في الفن
تمثيل الظلال في الفن منذ نشأته ، سمح بزيادة الشعور بالواقعية وبالعمق في الرسومات. ويمكن أن يعزى اول استخدام للظلال في تاريخ الرسم إلى مازاتشو (Masaccio)، حيث الاشكال تبدو أحجام حقيقية.
أنواع الظلال
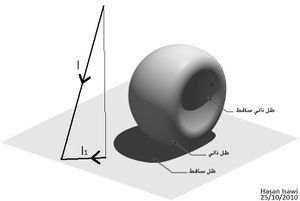
وفقاً للسطح (أو السطوح) الذي يستقبل الظل بالنسبة للجسم الماخوذ في الاعتبار, هناك ثلاثة تسميات للظلال، وهي:
- ظل ذاتي (بالإيطالية:ombra propria): هذا هو الجزء من K الغير معرض للضوء.
- ظل ساقط (بالإيطالية:ombra portata): هو اسقاط لحدود الظل الذاتي على الأسطح المجاورة.
- ظل ساقط ذاتي (بالإيطالية:ombra autoportata): هو إسقاط لحدود الظل الذاتي على سطح نفس الجسم K.
خلفية علمية
في الفقرات التالية، هناك خلفية علمية (اسقاطية) أتاحت للهندسة الوصفية رسم الظلال في طرق الاظهار المختلفة (منظور, اكسنومتري, مونج). أي الانشاءات الهندسية التي تأخذ في الاعتبار الاحتياجات الحقيقية عند ممارسة الرسم.
بالإضافة إلى المواضيع المتعلقة بإجراءات الرسم التقليدي، يتناول هذا النص التطورات الراهنة لنفس الموضوع. الذي مع ظهور أدوات الرسم الرقمي, لا يستخدم تلك الاجراءات في عدة إسقاطات فردية، ولكن من خلال عمليات اسقاط تلقائية لاي أي شكل من الأشكال على أي سطح. هذة العمليات تنفذ على نموذج افتراضي من واحد أو أكثر من مصادر الضوء, التي من الممكن انشائها في العديد من برامج الكمبيوتر المختصة. وبالإضافة إلى ذلك، في الحاسوب، أثر التصيير (Rendering) [9] يسمح بدراسة مفصلة للمواد وكيف تتصرف عند التعرض للضوء وتشكيل الظل. وبالتالي على ما يبدو مواجهة هذة الإجراءات الرسومية غير ضرورية، ولكنها تسمح للمصمم إدارة واعية للظلال المتولدة تلقائياً, والتحكم بمنطق البرنامج المستخدم، وإلا فهو غير قادر على التدخل لاجتياز العقبات التي, كما هو معروف ، تظهرها كل الادوات. هذه العقبات تؤدي الى اعتماد الخيارات والحلول الوسط للوصول, في الحالات المختلفة, الى تحقيق نتائج مفروضة: لهذا يجب معرفة المفهوم وتطبيقاته من أجل اتخاذ قرار الحل المناسب لكل حالة.
وعلاوة على ذلك ، الظلال تثري رسم السكتشات السريعة لإعطاء الفكرة الاولية لمشروع ما. والتي بعد ذلك ستحدد بدقة من خلال النمذجة الرقمية. كما في هذه الحالة, للحصول على رسومات واقعية، هناك الحاجة إلى معرفة كيفية تحديد ظل الأشكال والتكوينات المكانية الأكثر شيوعا.
غالبا الظلال تسمح باستكمال المعلومات ثلاثية الأبعاد لشكل ما، لأنها تعتبر رؤيا من مركز إسقاط أخر، أي أن هناك اسقاطين لنفس الشكل: مركز الاسقاط الاول يتطابق مع مركز النظر والاخر مع مصدر الضوء. في كلتا الحالتين ، من الضروري معرفة مفاهيم "عمليات الاسقاط والتقاطع" (operazioni di proiezioni e sezioni) لضمان تحقيق النتائج المرجوة. أو السماح لأفضل قراءة لنتائج الرسم واستبعاد غير مفهومة ومتناقضة أحيانا وغير ملائمة في كثير من الأحيان من من وجهة نظر جمالية.
تطبيقات الظلال في الاظهار تسمح بانشاء الرسم التقني مثل الخطة الحجمية (Volumetric plan) حيث تراكب الظل والخطة يعطي المعلومات المفقودة, ألا وهي ارتفاعات الاشكال الممثلة. ويمكن استخدام الظلال لزيادة تاثير وهمية البعد الثالث في الخطة والعلو ، والاكسنومتري والمنظور. والتي يمكن الحصول عليها بواسطة الرسم التقليدي او الرقمي.
الأسس الاسقاطية
العناصر المرجعية هي مصدر الضوء الذي تتفرع منة أشعة الضوء ( والتي للتبسيط تعتبر خطوط مستقيمة)، الشكل الذي يستقبل الضوء والمستوى حيث يقع الظل. كفاف الظل لشكل ما , يعرف كمحموعة من نقط تقاطع أشعة الضوء الماسة ذلك الشكل مع المستوى المتلقي للظل. لرسم الظلال ضروري تحديد "الخط فاصل الظل" الذي يشير إلى الخط الذي يفصل بين منطقة الظل ومنطقة الضوء لمجسم ما. إسقاط الخط فاصل الظل على سطح، يحدد كفاف "الظل الساقط" على نفس السطح. يمكن اعتبار الخط فاصل الظل كالكفاف الظاهر بالنسبة لمركز نظر متطابق مع مصدر الضوء. الذي يمكن ان يكون نقطة لانهائية مثل الشمس ، وفي هذه الحالة أشعة الضوء تكون موازية لبعضها البعض, أو انها تتقارب، عندما يكون مصدر الضوء نقطة نهائية مثل المصباح. ومن الممكن تمييز "الظل الذاتي الساقط" بظل الكيان الذي يقع على سطح نفس الكيان.
يمكن ملاحظة أنه لا توجد مناطق في الظل تماما أو في الضوء تماما ، ولكن هناك تدرجات من الضوء الى الظل. قانون جيب التمام او قانون لامبرت يحدد العلاقة بين كثافة الضوء لسطح ما والزاوية بين الأشعة الضوئية مع الخطوط العمودية على نفس السطح. يمكن ايجاد تطبيقات لهذا القانون في اظهار مستويات مختلفة الميلان بالنسبة لمصدر ضوء, او في تدريج كثافة الضوء على سطح منحني.
في الواقع ، كثيرا ما يحدث أن كيان يتلقى الضوء من مصادر مختلفة. وهذا يعني أن هناك مناطق من الكيان تتلقى ضوء من كل المصادر، والبعض من مصدر واحد والبعض الآخر لا يتلقى أي ضوء. في هذه الحالة يمكن ملاحظة الكرة مضائة من مصدر واحد (شكل) ، ثم الكرة نفسها تظهر آثار الإضاءة المجموعة (الشكل) من مصدرين ضوء مختلفين S1 و
الظل والهندسة الاسقاطية
قبل مواجهة بعض الإجراءات لتحديد الظل في الطريقة التقليدية (أو من خلال الرسم ثنائي الأبعاد *) , فانة مثير للاهتمام ، دون اعتبار اداة الرسم المستخدمة ، معرفة ان تكوين الظل يكمن في العلاقة التي تنشأ بين الشكل في الفراغ ومسقطة على مستوى ما. حيث مصدر الضوء في هذه الحالة يتطابق مع مركز الإسقاط.
لذلك في الفقرات التالية سوف نتعامل مع تشكيل الظل دون الاخذ في الاعتبار طريقة تمثيلها في أساليب الاظهار المختلفة (مونج, اكسنومتري,منظور) والتي ستناقش لاحقاً.
تحديد كفاف ظل لشكل ما يعتمد على نفس المبدأ الاسقاطي الذي هو أساس أساليب الاظهار المختلفة. مثلاً الإسقاط P' لنقطة P , على مستوى π , من مركز S , يُحدد بواسطة عمليات الاسقاط والتقاطع. أي, الإسقاط في عملية إيصال النقطتين P و S ؛ والتقاطع في ايجاد نقطة التقاطع P' بين الخط P - S والمستوى π. اذا استبدلنا مركز الإسقاط C بمصدر الضوء S, والظل P* بالاسقاط P' يمكننا ملاحظة أن عملية تحديد الظل مطابقة لعملية الإسقاط.
والإشارة إلى التشابه بين الظل والإسقاط ، فيمكن اعتبار الظل الناتج عن مصدر طبيعي (والذي يفترض أنة يقع في اللانهاية) إسقاط متوازي ( او اسطواني), مثل طريقة مونج, الاكسنومتري والمنظور، في حين ان الظل الناتج عن مصدر ضوء اصطناعي يمكن اعتباره إسقاط مركزي (او مخروطي), مثل الاسقاط المنظوري.
هذا التمييز مفيد لاعتماد نظام الإسقاط المناسب في تتبع كفاف الظل الساقط. والتي يمكن اعتبارها في أساليب الإظهار المختلفة كعملية إسقاط في الإسقاط.
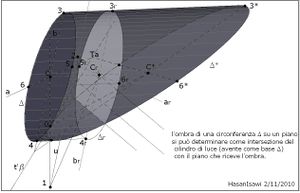
عند التحقق من وجود علاقة اسقاطية بين العناصر المتورطة في إيجاد الظل ، يمكن تحديد العلاقة بين الكائن وظله. العلاقة بين شكل مسطح ∆ وظلة ∆* تعتبر تقابل تألفي (او افّيني) عندما يكون مصدر الضوء نقطة لانهائية ، حيث محور التقابل هو خط التقاطع بين مستوى الشكل ∆ والمستوى الذي يتلقى الظل، ومركز التقابل هو مصدر الضوء نفسه. بينما اذا كان المصدر نقط نهائية ، لا تتغير عناصر التقابل التي هي المحور u والمركز U, ولكن التناظر يسمى تقابل منظوري. بمجرد الانتهاء من تحديد متطلبات التقابل : المركز U والمحور u ونقطتين متقابلتين (أو خطين متناظرين) ، يمكن المضي قدما لتحديد نقاط ظل أخرى من خلال استغلال خاصية التقابل ، التي تكمن في اصطفاف النقاط المتناظرة مع المركز U وفي تقابل الخطوط المتقابلة على طول المحور u. على سبيل المثال ، بمجرد إيجاد نقطتين متقابلتين مثل A* و A (الشكل --)، يمكن تحديد الظل B*: (للنقطة B ) بتوصيل النقطتين A و B بواسطة الخط r , الذي يلتقي المحور u في النقطة t'α. والتي بتوصيلها A* نجد الخط r* ( ظل الخط r ) , الذي يتقاطع في النقطة B* (نقطة الظل المطلوبة) مع شعاع الضوء المار بالنقطة B .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
الظل كعملية تقاطع بين كيانات هندسية
يمكن تفسير الظل كعملية تقاطع بين كيان ضوئي مع كيان متلقي للظل. الكيان الضوئي يمكن أن يكون خط في الحالة التي يراد فيها إيجاد ظل نقطة , ويمكن ان يكون سطح مستوي أو منحني عندما يراد إيجاد ظل خط مستقيم أو منحني. ويمكن صياغة هذه الحالات كالنحو التالي :
- ظل نقطة P على سطح ∆ يمكن تحديده كنقطة تقاطع بين الشعاع الضوئي المار بالنقطة P مع السطح المتلقي الظل ∆
- ظل خط مستقيم r على سطح ∆ يعادل تقاطع بين مستوى ضوئي مار بالخط r والسطح ∆.
- ظل مضلع θ على سطح ∆, يعادل تقاطع بين منشور ضوئي والسطح ∆. حواف المنشور تتكون من أشعة الضوء وقاعدته تتطابق مع نفس المضلع θ.
- ظل خط منحنى κ على سطح مستو α، يتوافق مع تقاطع بين اسطوانة ضوئية والسطح α . سطح الاسطوانة تتكون من أشعة الضوء وقاعدته تتطابق مع نفس المنحنى κ.
أمثلة
في الفقرات التالية هناك أمتله لبعض حالات التقاطع بين كيان ضوئي وكيان متلقي للظل.
ظل نقطة P على سطح مستوي ( أو منحني) كتقاطع بين شعاع الضوء والمستوي
مثال 1: ظل نقطة على مستوى عام
يتم تحديد ظل نقطة P على مستوى عام α (ألفا) كنقطة تقاطع بين شعاع الضوء المار بالنقطة P والمستوى المتلقى الظل α. لتحديد ؛* كظل للنقطة P يجب فهم واتباع الإجراءات التالية:
- 1- نمرر بالنقطة P شعاع ضوئي l
- 2- نمرر بشعاع الضوء l مستوى مساعد رأسي λ
- 3- نحدد خط التقاطع بين المستويات ألفا وبيتا
- 4- في النهاية نجد نقطة التقاطع P* (وهو المطلوب) بين الخطوط r و s.
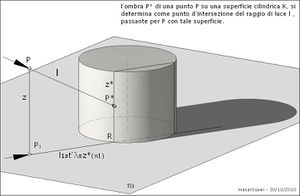
مثال1(1): ظل نقطة على سطح اسطواني بمحور رأسي
يتم تحديد ظل نقطة P على مستوى اسطواني K كنقطة تقاطع بين شعاع الضوء المار بالنقطة P وذلك السطح المتلقى الظل. لتحديد ظل النقطة P ينبغي اتباع الاجراءات التالية:
- – نمرر بالنقطة P شعاع ضوئي l
- -- نمرر بشعاع الضوء l مستوى مساعد رأسي λ
- – نحدد خط التقاطع z* بين المستوى المساعد لامدا والسطح K
- -- في النهاية نجد نقطة التقاطع P* (وهو المطلوب) بين الخطوط z* و s.
ملاحظة : لتسهيل بشكل عام ، تحديد ظل نقطة P على سطح أسطواني K، خصوصاً في الرسم التقليدي (اي ثنائية الأبعاد), من الأفضل اختيار خط g موازي لمحور الاسطوانة, لأن ظل g سيكون موازي لمحور الأسطوانة. للحصول على ظل g في هذه الطريقة, ينبغي تحديد نقطة التقاطع Q للخط g مع مستوى قاعدة الاسطوانة. ثم تحديد ظل نقطة ثانية ( مثل P) لايجاد ظل الخط m على نفس مستوى القاعدة. بتوصيل النقاط R و P*(δ) نجد m*(δ (ظل m على مستوى القاعدة). نتابع بإيجاد نقطة التقاطع R بين الخط m*(δ وقاعدة الاسطوانة. ومن هذة النقطة R نرسم g* ظل الخط g على السطح الاسطواني بحيث يكون, كما قلنا سابقاً, موازي لمحور الاسطوانة. وأخيراً نجد النقطة P* كما هو مطلوب , كتقاطع بين الشعاع الضوئي المار بالنقطة P والخط m*.
ظل دائرة ∆ على سطح مستوي 1π يمكن أن يُحدد كتقاطع بين اسطوانة ضوء (بقاعدة ∆) مع المستوى 1π لذي يتلقى الظل.
مثال 3: ظل نقطة على سطح مخروطي
ظل نقطة P على سطح، سواء مستوي أو منحني ، يتم بتحديد نقطة التقاطع بين شعاع الضوء المار بالنقطة P وذلك السطح المتلقى الظل.
- منذ ان نقطة التقاطع P (ظل النقطة P) تحدد باستخدام مستوى ضوء λ يمر بالنقطة P ويتقاطع مع السطح المتلقى الظل وفقاً لخط , الذي يمكن ان يكون مستقيم أو منحني. في الحالة التي يكون فيها السطح مستوي ، يسهل تحديد خط التقاطع, ويصعب تحديدة في حالة السطح المنحنى ، على الأقل في الرسم التقليدي (أو بالأحرى في الرسم ثنائي الأبعاد).
في هذه الحالات ، ولتسهيل عمليات الانشاءات الهندسية, هناك الحاجة إلى معرفة الخصائص الهندسية للسطح المعني، أو بالاحرى معرفة ماهية التكوين الهندسي لذلك النوع من الاسطح ، من أجل الحصول، إذا ممكن ، على مقاطع سهلة التحديد. على سبيل المثال ، في حالة السطح المخروطي، المقاطع الأكثر بساطة تتكون من خطوط مستقيمة, يحصل عليها باستخدام مستويات مارة بقمة ذلك السطح. الأسطح المخروطية تشمل جميع أنواع المخاريط (بما في ذلك الاسطوانة كحالة خاصة للمخروط) التي تسمح بايجاد في كل نقطة منها مقطع مخروطي (بما في ذلك النقطة ، والخط كحالات اسثنائية للمخروطيات). بالاشارة الى المسألة في الشكل ، ظل نقطة P ، او بالاحرى نقطة تقاطع بين شعاع الضوء المار بالنقطة P والمخروط K , يحدد باستخدام مستوى ضوء λ بحيث يمر بالنقطة P وبقمة المخروط. بهذة الطريقة, المستوى λ يقطع المخروط وفقاً لخطيين. التي يمران بقمة K وبالتوالي بنقطتين من قاعدة K. للعثور على هذه النقاط يجب علينا تحديد خط التقاطع P*-V* , (والذي في هذه الحالة يتطابق مع الاثر الاول للمستوى λ) بين مستوى الضوء λ ومستوى القاعدة π1 , الخط P*-V*. يحدد من النقطتان P* و V*, والتي تمثل بالتوالي، P* ظل النقطة المعينة على مستوى القاعدة و V* ظل القمة نفس المستوى. حيث الخط P*-V* يقطع القاعدة نجد النقطتان R Q , بتوصيل هاتان النقطتان بالقمة نجد خطان التقاطع بين المخروط ومستوى الضوء λ . وأخيرا نجد النقطة المطلوبة P* ( ظل النقطة P) كتقاطع بين خط الضوء l وخط التقاطع V*-R (راسم سطح المخروط).
مثال 3: ظل نقطة على سطح كروي
ظل خط مستقيم r على سطح مستوي ( أو منحني)
مثال 1: ظل خط عام r على مستوى عام α
لتحديد ظل الخط r على المستوى α ، ينبغي تحديد ظل نقطتين من r على α
- 1- لتحديد ظل النقطة الأولى P ، نبدأ على النحو التالي :
- - ظل النقطة P يُحدد كنقطة تقاطع بين شعاع الضوء l المار بالنقطة P والمستوى α . للقيام بذلك - نمرر بالشعاع l مستوى رأسي β , - نحدد خط التقاطع s بين المستويين β و α . وهكذا نجد P* ( ظل P) كنقطة تقاطع بين الخط s والشعاع l.
- 2- لتحديد ظل نقطة ثانية للخط r على α ، يمكننا ان نتابع كما يلي :
- - نجد ظل الخط r على π1 (مستوى الإسقاط الأول) بتحديد وتوصيل النقطتين T’r ( الأثر الأول للخط r) و P*(p1) (ظل النقطة P على π1) . من المهم ملاحظة ان ظل الخط r على π1 يمثل خط تقاطع مستوى الضوء λ المار بالخط r مع π1, والذي يسمى الأثر الأول للمستوى λ ويرمز له t'λ.
- - نجد نقطة التقاطع R بين الآثار الأولى (t'α و t'λ ) للمستويات α و λ . النقطة R تمثل ظل نقط ثانية للخط r على المستوى α. لذلك نجد r* (ظل الخط r على α), بتوصيل النقطتين P* و R . وأخيراً, نجد Q* (ظل الطرف الأخر للخط r) كنقطة تقاطع بين r* وشعاع الضوء المار بالنقطة Q
ظل شكل مستوي على سطح مستوي كتقاطع بين سطح ضوء والمستوي
مثال1 : ظل دائرة ∆ على سطح مستوي 1π يمكن أن يحدد كتقاطع بين اسطوانة ضوء (بقاعدة ∆) مع المستوى 1π لذي يتلقى الظل
نتائج
قد يكون على حق, جزئياً ، من يقول ان إنشاء ظلال النماذج الافتراضية يتم تلقائيا ، وأنة كافي معرفة القليل من قواعد الهندسة الوصفية للحصول على نتائج اظهار مقنعة. ولكن يجب أن يكزن لدينا رؤية أوسع للاقتناع بحقائق أخرى. ينبغي أن نتذكر دائما الغرض الرئيسي من تدريس الهندسة الوصفية ، متجاوزون تلك التقنيات الهادفة إلى حل مشكلة هندسية معينة, ألا وهو ممارسة العقل على إدراك الفراغ والسيطرة بشكل دقيق على أشكاله الممكنة وأساليب اظهارة المختلفة. وبما ان فكرة التصميم تنبع في المقام الأول من خبرة وتجربة العقل ، فان تدريس الهندسة الوصفية يجد ما يبرره اذا كان الهدف هو تدريب هذا العقل على التفكير في كيفية عرض فكرة تصميمية معينة والتحقق من ميزاتها الهندسية والإدراكية. وعلاوة على ذلك ، وبالاتفاق مع من يقول أن الصورة تساوي ألف كلمة ، أود أن أؤكد على أن إنشاء تلك الصورة كان قد مر بمراحل من التفكير والمناقشة مليئة بالآلاف من الكلمات. وبهذا أريد ان ا قول إن هناك حاجة ماسة الى معرفة اللغة الخاصة بالهندسة الوصفية لتنظيم ومناقشة العديد من الشكوك التي عادة ما تتشكل عند انشاء وإظهار الأشكال الهندسية المختلفة وتكويناتها أللانهائية.
ولكي أكون أكثر قناعة ، على الأقل بالنسبة لأولئك المتشككين بفائدة الهندسة الوصفية، أود التأكيد ان مفاهيم وطريقة عمل الهندسة الوصفية ، تسمح من الناحية التقنية بتنفيذ الإنشاءات الهندسية المختلفة في مراحل إعداد عمليات توليد النماذج ثلاثية الأبعاد ومن ثم في تعيين أساليب الاطهار المناسبة.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
معرض صور
مصادر
- ^ [ماريو دوتشي (M.Docci) ، دليل التصميم المعماري (Manuale di disegno architettonico). ]
- ^ J.F. Heather. 1851. An elementary treatise on descriptive geometry, with a theory of shadows and of perspective
- ^ [Barnabé Brisson. G Monge. "Geometrie descriptive". argomentee d'una theorie des ombres et de la perspective. gauthier villiars. 1820]
- ^ [Louis Vallée, Traité de la science du dessin, contenant la théorie générale des ombres, la perspective linéaire, la théorie générale des images d'optique, et la perspective]
- ^ [JPN Hachette, 1828. Traité de Géométrie Descriptive: Comprenant les Applications de Cette Géométrie Aux Ombres, À la Perspective et À la Stéréotomie.]
- ^ [JJ Pillet, Traité de perspective linéaire ... ombres usuelles et du Rendu dans le dessin d'architecture e dans le dessin des machines, Paris - Leipzig,Blanchard, 1885-1921]
- ^ [Domenico Tessari, La Teoria delle ombre e del chiaro-scuro, Ulrico Hoepli, Milano 1921]
- ^ [Elia Bonci, teoria delle ombre e del chiaroscuro, Hoepli 1937.]
- ^ [تصيير (باللغة الإنجليزية Rendering) تشير بشكل عام الى الأداء في الرسم ، أو عملية يقوم بها الرسام لانتاج اظهار ذات جودة لكيان هندسي (في التصميم أو المسح). في الآونة الأخيرة نسبيا أصبحت كلمة أساسية في نطاق رسومات الحاسوب ، والتي تحدد عملية توليد صورة لمشهد ثلاثي الابعاد , بالاعتماد على خوارزميات تحدد لون كل نقطة في الصورة, وعلى معلومات رياضية عن هندسة الشكل ، مركز النظر ، و الخصائص الضوئية للأسطح المرئية وعن مصدر الضوء]
طالع أيضاً
- Problemi di incidenza
- problemi di misura
- problemi di reciproche posizioni